2 Comparative visualization
A classification of approaches in comparative visualization is presented in [3]. These early examples emphasize the image level comparison. Data from different sources is displayed side by side using similar visualization technique to support straight forward comparison. Fig. 2 shows a comparison of the structured grid as it is generated from the geometry generation step compared to the unstructured tetrahedral CFD grid of an aircraft seen from the top as it is used for the numerical flow simulation. Note the different clustering of grid points which illustrates the flexibility of the grid generation tools to increase numerical accuracy in regions of interest.
Fig. 2 Side by side comparison of the curvilinear grid from the geometry generation tool and the unstructured CFD grid. The configuration shows the wing-root section of an high wing aircraft from the top.
A more elaborate image level comparison is obtained from performing pixel operations on the comparable images. For example, experimental Schlieren images may be superimposed on simulated Schlieren images of numerical flow solutions using a colour mapping [3].
This techniques allows to precisely visualize and quantify properties in the data such as the spatial displacement of features like a shock wave. The concept was extended to the use of skin-friction lines in comparative visualization [4] and simulation of oil-flow pattern [5][4].
Image level comparison often requires dedicated algorithms to simulate optical image acquisition techniques used in experimental fluid dynamics. Recently this technology called Computational Flow Imagery CFI attracts increasing attention. [5]. Comparative visualization for surface attributes on a given surface was examined by Pang anf Freeman. [6]
There are cases, however when differences between images are difficult to distinguish or more quantitative information is called for. This gives rise to a second type of comparative visualization which requires the differences between data of various sources to be evaluated on the data level. These differences are then visualized.
For example, various geometry definition codes employ different algorithms to ensure curvature of surfaces. The smoothness of the surface needs to be well adjusted to the requirements of the flow simulation code in order to run the flow simulation efficiently. It is very difficult to identify the differences between geometries generated from different codes. The differences are usually hard to detect for the human eye.
In order to perform data level comparison, the Euclidean distance between two geometries of choice is determined for each node-point on the surface. This data is then mapped onto the geometry.
Fig. 3 Wing-body junction of a high wing aircraft. Colors denote the Euclidean distance of two aircraft shapes to be compared.
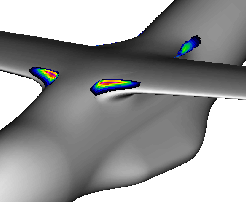
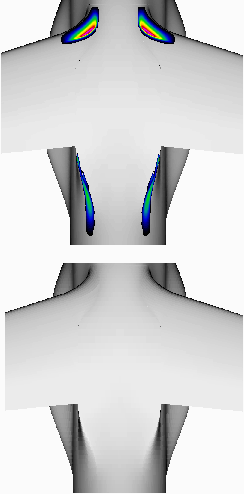
This data level comparison extracts regions of interest, in this case the leading edge and trailing edge part of the wing-body junction (Fig. 3). After performing this step of extracting the regions of geometry change one may well examine the geometry by using traditional visualization. Fig. 5 presents the data level comparison in the top view compared to a side by side comparison of the two geometries of choice in a flat shaded display. By careful selection of the illumination the different curvature becomes visible near the left trailing edge. However, the data level comparison is obviously more useful and easier to interpret as may be seen in the upper image.
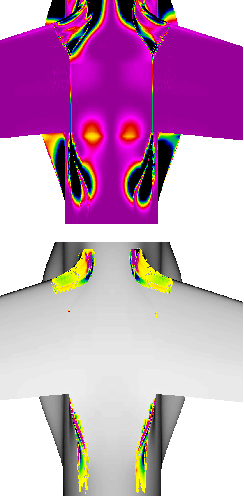
In cases of comparison between interpolated geometries an analysis of spatial distances may be obscured by noise in the data. In such a case the comparison of the local curvature of the surface provides a better tool in particular when looking for the quality of surfaces to be used for CFD analysis. Fig. 5 illustrates a side by side comparison of local surface curvature as well as a data level comparison of curvature difference between the right and left aircraft geometry.
Data level comparison was successfully applied to results of numerical flow simulations as well. One way to perform the comparison uses a similar approach as for the comparison of geometries.
Fig. 4 Top view of a comparative visualization of two slightly varying geometries. Euclidean distances displayed in the top image, side by side comparison in the bottom image (left and right half of the aircraft shape).
Comparative data may be obtained by performing algebraic operations to combine the two data sets to be compared.
For example a quantity such as the density of the flow fields may be compared at every position in physical space by substracting the density values of the two data sets and displaying their difference.
Fig. 5 Top view of a comparative visualization of two slightly varying geometries. Curvature is displayed in the top image in a side by side comparison and the curvature difference is projected onto the surface in the bottom image.
Another method of comparative visualization combines extracted features from different data sources into a single image. In aerodynamic aircraft design the position of supersonic regions on top of a wing plays a key role. This position depends on many parameters. It may be visualized by displaying the iso-surface of Mach number equal to 1. Fig. 6 shows the shape of the supersonic region as a result of varying flow parameters, in this case a change in angle of attack.
Fig. 6 Isosurface for Machnumber equal to 1 for to different angles of attack. The two colors identify the different flow cases.
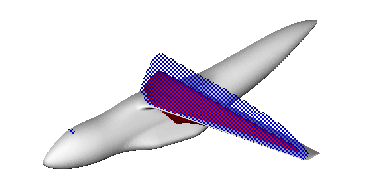
The smaller angle of attack is shown by the red iso-surface while the larger angle results in the blue surface. Note the small supersonic flow region which occurs on top of the canopy in the case of larger flow angle.




